Topological Sort

Topological Sort 是一種在有向無環圖（DAG）中對節點進行排序的算法。

它通常應用於解決依賴關係的排序問題，例如項目排程或任務排程等。

拓撲排序的目標是確保在排序結果中，任何一條有向邊 的起點節點 都位於終點節點 的前面，這樣就能確保沒有循環依賴關係。

拓撲排序的算法主要包括以下步驟：

1. 選擇一個 in-degree 為0的節點，這些節點可以視為起始節點。
2. 將該節點添加到排序結果中。
3. 刪除這個節點以及所有以該節點為起點的邊。
4. 重複步驟1至步驟3，直到所有節點都已添加到排序結果中或者無法找到入度為0的節點為止。

如果最終排序結果包含了所有的節點，那麼這個排序就是有效的。

如果圖中存在循環依賴關係，則拓撲排序無法成功完成，因為無法找到入度為0的節點。

// Topology sort using DFS in Kotlin

import java.util.Stack

class Graph(private val n: Int) {
    private val adj: Array<MutableList<Int>> = Array(n) { mutableListOf() }

    fun addEdge(u: Int, v: Int) {
        adj[u].add(v)
    }

    private fun dfs(v: Int, visited: BooleanArray, stack: Stack<Int>) {
        visited[v] = true
        for (i in adj[v]) {
            if (!visited[i]) {
                dfs(i, visited, stack)
            }
        }
        stack.push(v)
    }

    fun topologicalSort(): Stack<Int> {
        val visited = BooleanArray(n)
        val stack = Stack<Int>()
        for (i in 0 until n) {
            if (!visited[i]) {
                dfs(i, visited, stack)
            }
        }
        return stack
    }
}

fun main(args: Array<String>) {
    val g = Graph(6)
    g.addEdge(5, 2)
    g.addEdge(5, 0)
    g.addEdge(4, 0)
    g.addEdge(4, 1)
    g.addEdge(2, 3)
    g.addEdge(3, 1)
    val stack = g.topologicalSort()
    while (!stack.isEmpty()) {
        print(stack.pop().toString() + " ")
    }
}

Dijkstra's Algorithm

Dijkstra's Algorithm 是一種用於找尋最短路徑的計算方法，通常應用在圖形。

演算法

1. 起始點設定：
   選擇一個起始節點，並將其距離設為零。這個節點代表我們的出發點。
2. 初始化距離：
   對於所有其他節點，將它們的距離初始化為無限大，表示我們不知道它們到達起始節點的最短距離。
3. 選擇最近節點：
   從未訪問過的節點中選擇距離起始節點最近的節點。這個節點將被標記為已訪問。
4. 更新鄰居節點的距離：
   對於選擇的節點，計算它的所有相鄰節點到起始節點的距離。如果通過選擇的節點前往某個鄰居節點的距離比當前已知的距離更短，則更新該鄰居節點的距離。
5. 重複步驟3和步驟4：
   重複選擇最近節點並更新鄰居節點的距離，直到所有節點都被訪問過或無法到達。
6. 最短路徑計算：
   當所有節點都被訪問過或無法到達時，我們就得到了從起始節點到每個節點的最短距離。
7. 路徑重建（可選）：
   如果需要找到從起始節點到某個特定節點的最短路徑，可以從終點節點開始，根據每個節點的距離和前驅節點，反向重建路徑。

Dijkstra's Algorithm 通常應用於帶有權重的有向圖，用於解決最短路徑問題。

它確保了找到的最短路徑是基於已知的權重訊息，並且不包含負權重的循環。

// Dijstra algorithm in Kotlin
class Dijkstra {
    private val graph: Array<IntArray>
    private val n: Int
    private val dist: IntArray
    private val visited: BooleanArray

    constructor(graph: Array<IntArray>, n: Int) {
        this.graph = graph
        this.n = n
        dist = IntArray(n)
        visited = BooleanArray(n)
    }

    fun dijkstra(start: Int) {
        for (i in 0 until n) {
            dist[i] = Int.MAX_VALUE
            visited[i] = false
        }
        dist[start] = 0
        for (i in 0 until n - 1) {
            val u = minDistance(dist, visited)
            visited[u] = true
            for (v in 0 until n) {
                if (!visited[v] && graph[u][v] != 0 && dist[u] != Int.MAX_VALUE && dist[u] + graph[u][v] < dist[v]) {
                    dist[v] = dist[u] + graph[u][v]
                }
            }
        }
        printSolution(dist, n)
    }

    private fun minDistance(dist: IntArray, visited: BooleanArray): Int {
        var min = Int.MAX_VALUE
        var minIndex = -1
        for (v in 0 until n) {
            if (!visited[v] && dist[v] <= min) {
                min = dist[v]
                minIndex = v
            }
        }
        return minIndex
    }

    private fun printSolution(dist: IntArray, n: Int) {
        println("Vertex Distance from Source")
        for (i in 0 until n) {
            println(i.toString() + ": " + dist[i])
        }
    }
}

// main function
fun main(args: Array<String>) {
    val graph = arrayOf(intArrayOf(0, 4, 0, 0, 0, 0, 0, 8, 0),
            intArrayOf(4, 0, 8, 0, 0, 0, 0, 11, 0),
            intArrayOf(0, 8, 0, 7, 0, 4, 0, 0, 2),
            intArrayOf(0, 0, 7, 0, 9, 14, 0, 0, 0),
            intArrayOf(0, 0, 0, 9, 0, 10, 0, 0, 0),
            intArrayOf(0, 0, 4, 14, 10, 0, 2, 0, 0),
            intArrayOf(0, 0, 0, 0, 0, 2, 0, 1, 6),
            intArrayOf(8, 11, 0, 0, 0, 0, 1, 0, 7),
            intArrayOf(0, 0, 2, 0, 0, 0, 6, 7, 0))
    val t = Dijkstra(graph, 9)
    t.dijkstra(0)
}

以下是圖的部分

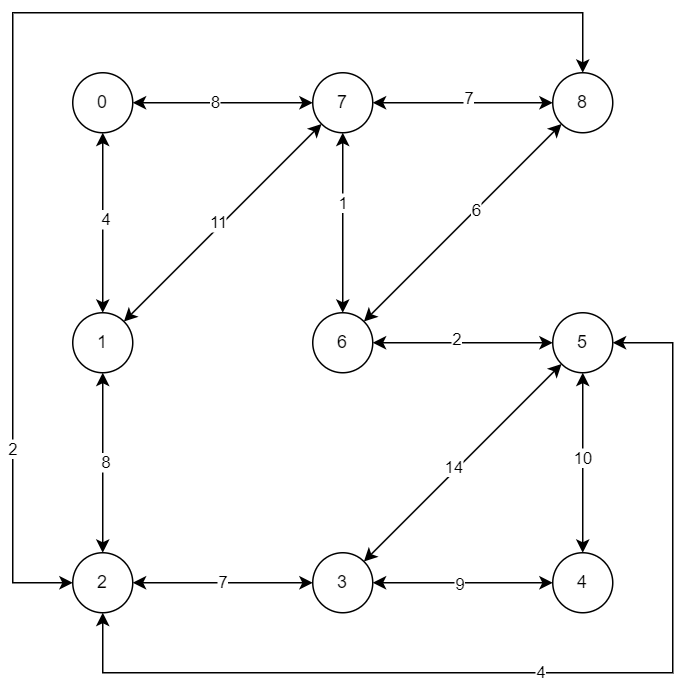
演算法輸出為

Vertex Distance from Source
0: 0
1: 4
2: 12
3: 19
4: 21
5: 11
6: 9
7: 8
8: 14

所有 Code 可以在 Github 找到 ～

感謝各位觀看我文章的人 !!!

明天會接著介紹 Bellman-Ford Algorithm 和 Floyd-Warshall Algorithm

敬請期待 ~